Santiago Arango-Piñeros
Academic Website

• My office is LGRT 1238.
• santiago.arango.pineros@gmail.com
• sarangopiner@umass.edu
• santiago.arango@emory.edu
• Here are my arXiv papers, MathSciNet profile, and GitHub profile.

• I am co-organizing the Five College Number Theory Seminar with David Zureick-Brown.

The pdf versions are updated more frequently.

Counting number fields of fixed degree by their smallest defining polynomial,
with Fabian Gundlach, Robert J. Lemke Oliver, Kevin J. McGown, Will Sawin, Allechar Serrano López, Arul Shankar, and Ila Varma.


Counting primitive integral solutions to spherical generalized Fermat equations.
(pdf, 2508.13093, Magma experiment)

Fermat descent.
(pdf, 2508.13059)

Galois groups of simple abelian varieties over finite fields and exceptional Tate classes,
with Sam Frengley and Sameera Vemulapalli.
(2505.09589, code)

Counting 5-isogenies of elliptic curves over the rationals,
with Changho Han, Oana Padurariu, and Sun Woo Park.
(2504.07750, code)

Bounds for the relative class number problem for function fields,
with María Chara, Asimina S. Hamakiotes, Kiran S. Kedlaya, and Gustavo Rama.
Journal of Number Theory 278 (2026), 977-1010.
(DOI, MR 4927618, 2412.12467, code)

Galois groups of low dimensional abelian varieties over finite fields,
with Sam Frengley and Sameera Vemulapalli.
To appear in Transactions of the American Mathematical Society.
(2412.03358, code)

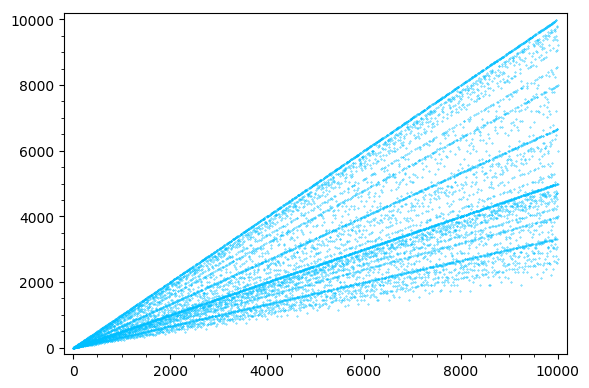
Frobenius distributions of low dimensional abelian varieties over finite fields,
with Deewang Bhamidipati and Soumya Sankar.
International Mathematics Research Notices 2024 (2024), no. 16, 11989-12020.
(2306.02237, code)

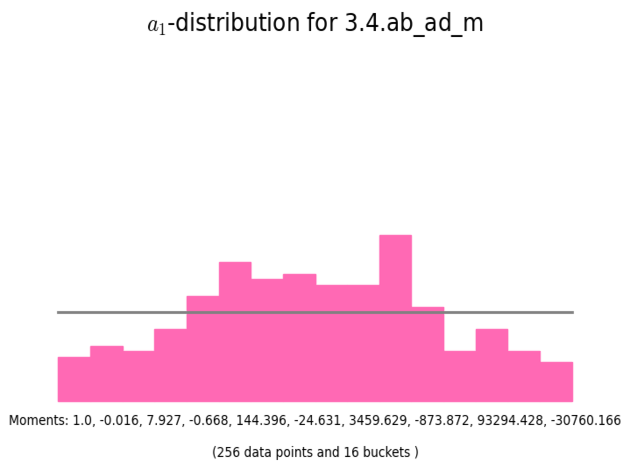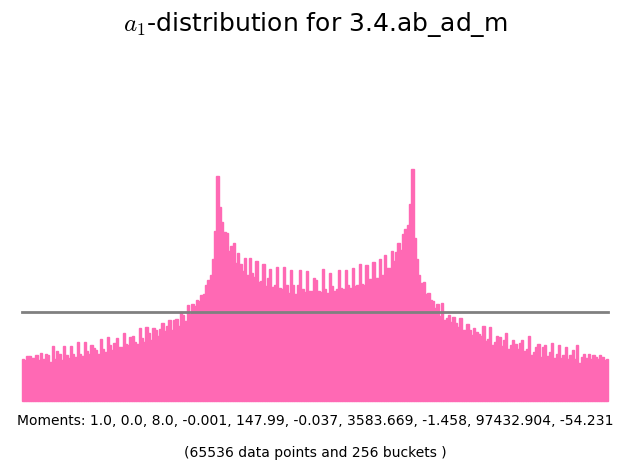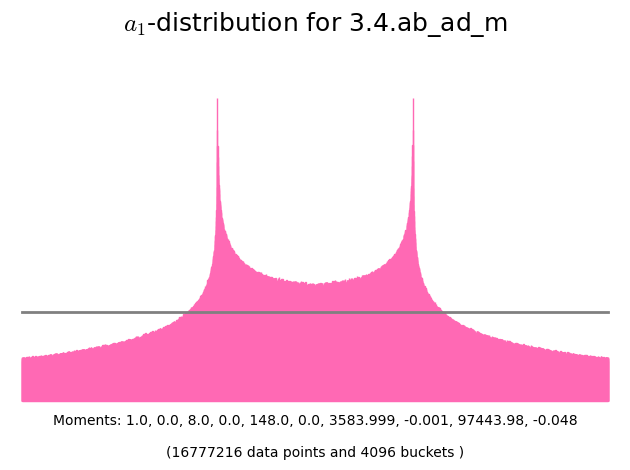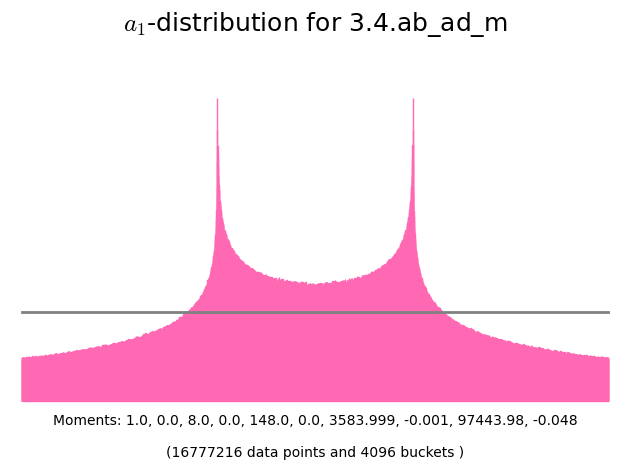
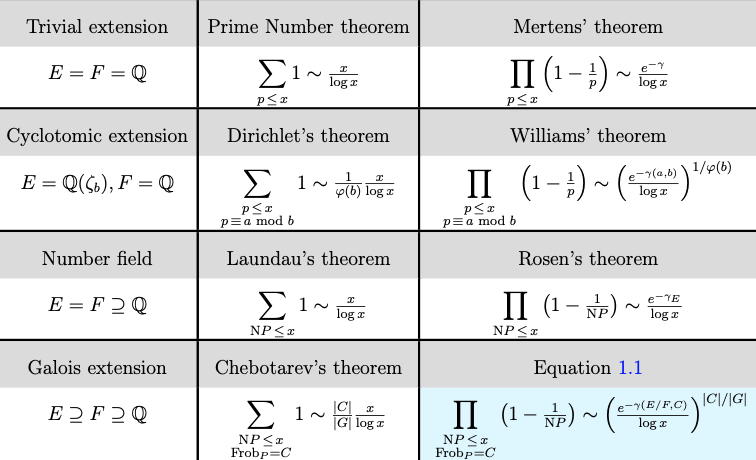
Mertens' theorem for Chebotarev sets,
with Daniel Keliher and Chris Keyes.
International Journal of Number Theory 18 (2022), no. 8, 1823-1842.
(MR 4439576, 2103.14747)

The global field Euler function,
with Juan Diego Rojas.
Research in the Mathematical Sciences 7 (2020), no. 3, Paper No. 19, 21 pp.
(MR 4123394, 2005.04521)